Bài tập Toán Lớp 11 - Luyện tập phương trình lượng giác
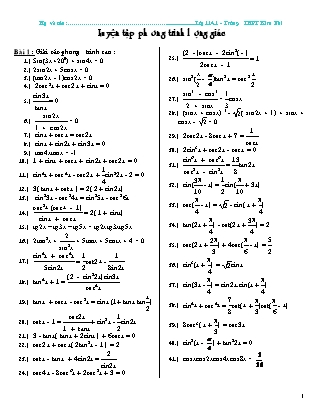
Bài 2 : Tìm nghiệm thuộc khoảng của phơng trình :
Bài 3 : Xác định m để phơng trình sau có nghiệm :
Bài 4 : Cho phơng trình : sin3x + cos3x = msinxcosx
a.) Giải phơng trình với m = 2
b.)Tìm m để phơng trình có nghiệm.
Bài 5 : Cho phơng trình :
a) Giải phơng trình với m = 2
b) Tìm m để phơng trình có nghiệm x ? [0 ; ?2 ]
Bài 6 : Tìm m để phơng trình : cos2x + (2m - 1)cosx + 1 - m = 0 có nghiệm x ? ( ?2 ; ?)
Bạn đang xem tài liệu "Bài tập Toán Lớp 11 - Luyện tập phương trình lượng giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Luyện tập phương trình lượng giác Bài 1 : Giải các phương trình sau : Sin(3x+200) + sin4x = 0 2sin2x + 5cosx = 0 (tan2x - 1)cos2x = 0 2cos2x + cos2x + sinx = 0 = 0 = 0 sinx + cosx = cos2x sinx + sin2x + sin3x = 0 tan4xtanx = -1 1 + sinx + cosx + sin2x + cos2x = 0 sin4x + cos4x - cos2x + sin22x - 2 = 0 3( tanx + cotx ) = 2( 2 + sin2x) sin23x - cos24x = sin25x - cos26x = 2( 1 + sinx) tg2x – tg3x – tg5x = tg2xtg3xtg5x 2tan2x + + 5tanx + 5cotx + 4 = 0 = cot2x - tan4x + 1 = tanx + cosx - cos2x = sinx (1+ tanx tan) cotx - 1 = + sin2x - sin2x 3 - tanx( tanx + 2sinx ) + 6cosx = 0 cos2x + cosx( 2tan2x - 1 ) = 2 cotx - tanx + 4sin2x = cos4x - 8cos6x + 2cos2x + 3 = 0 = 1 sin2( - )tan2x = cos2 = cosx (sinx + cosx) 3 - ( sin2x + 1) + sinx + cosx - = 0 2cos2x - 8cosx + 7 = 2sin3x + cos2x - cosx = 0 = tan2x sin( - x) = sin( + 3x) cos( - x) = - sin( x + ) tan(2x + ) - cot(2x + ) = 2 cos(2x + ) + 4cos( - x) = sin3(x + ) = sinx sin(3x - ) = sin2x.sin(x + ) sin4x + cos4x = cot(x + )cot( - x) 8cos3( x + ) = cos3x sin2(x - ) + tan22x = 0 cosxcos2xcos4xcos8x = sinx + sin2x +sin3x +sin4x = cot cosxcos2xcos3x – sinxsin2xsin3x = sin3xsin3x + cos3xcos3x = + cosx = 0 2sin( x + ) = + 8cos6x + 2sin3x sin3x - 6cos4x - 1 = 0 cos2x + 5 = 2( 2 - cosx )(sinx - cosx ) = 1 sin2x + sin23x = cos22x + cos24x 3tan3x- tanx + -8cos2( - )= 0 2sin3x - sinx = 2cos3x - cosx + cos2x tg2x + sin2x = cotgx = sinxcosx + cosx = - 2sin2x - sinx + 1 cos = cos2 sin2x + cos2x + tanx = 2 sin2x + sin22x + sin23x = 2 6sinx - 2cos3x = 5sin2xcosx Bài 2 : Tìm nghiệm thuộc khoảng của phương trình : Bài 3 : Xác định m để phương trình sau có nghiệm : Bài 4 : Cho phương trình : sin3x + cos3x = msinxcosx a.) Giải phương trình với m = b.)Tìm m để phương trình có nghiệm. Bài 5 : Cho phương trình : Giải phương trình với m = 2 Tìm m để phương trình có nghiệm x ẻ [0 ; ] Bài 6 : Tìm m để phương trình : cos2x + (2m - 1)cosx + 1 - m = 0 có nghiệm x ẻ ( ; p) -------------------Hết---------------------
Tài liệu đính kèm:
 bai_tap_toan_lop_11_luyen_tap_phuong_trinh_luong_giac.doc
bai_tap_toan_lop_11_luyen_tap_phuong_trinh_luong_giac.doc



