Đề kiểm tra Học kì 1 môn Toán Lớp 6 - Năm học 2020-2021 - Trường THCS Cao Bá Quát (Có đáp án)

PHÒNG GD&ĐT THUẬN BẮC
TRƯỜNG THCS CAO BÁ QUÁT
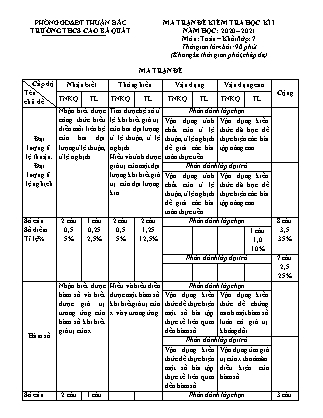
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I
NĂM HỌC: 2020 – 2021
Môn: Toán – Khối/lớp: 7
Thời gian làm bài: 90 phút
(Không kể thời gian phát, chép đề)
MA TRẬN ĐỀ
 Cấp độ
Tên
chủ đề
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Cộng
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Đại lượng tỉ lệ thuận. Đại lượng tỉ lệ nghịch
Nhận biết được công thức biểu diễn mối liên hệ của hai đại lượng tỉ lệ thuận, tỉ lệ nghịch.
Tìm được hệ số tỉ lệ khi biết giá trị của hai đại lượng tỉ lệ thuận, tỉ lệ nghịch.
Hiểu và tính được giá trị của một đại lượng khi biết giá trị của đại lượng kia.
Phần dành lớp chọn
Vận dụng tính chất của tỉ lệ thuận, tỉ lệ nghịch để giải các bài toán thực tiễn.
Vận dụng kiến thức đã học để thực hiện các bài tập nâng cao
Phần dành lớp đại trà
Vận dụng tính chất của tỉ lệ thuận, tỉ lệ nghịch để giải các bài toán thực tiễn.
Vận dụng kiến thức đã học để thực hiện các bài tập nâng cao
Số câu
Số điểm
Tỉ lệ%
2 câu
0,5
5%
1 câu
0,25
2,5%
2 câu
0,5
5%
2 câu
1,25
12,5%
Phần dành lớp chọn
8 câu
3,5
35%
1 câu
1,0
10%
Phần dành lớp đại trà
7 câu
2,5
25%
Hàm số
Nhận biết được hàm số và biết được giá trị tương ứng của hàm số khi biết giá trị của x
Hiểu và biểu diễn được một hàm số khi biết giá trị của x và y tương ứng
Phần dành lớp chọn
Vận dụng kiến thức để thực hiện một số bài tập thực tế liên quan đến hàm số.
Vận dụng kiến thức để chứng minh một hàm số luôn có giá trị không đổi
Phần dành lớp đại trà
Vận dụng kiến thức để thực hiện một số bài tập thực tế liên quan đến hàm số.
Vận dụng tìm giá trị của x thoả mãn điều kiện của hàm số.
Số câu
Số điểm
Tỉ lệ%
2 câu
0,5
5%
1 câu
1,0
10%
Phần dành lớp chọn
3 câu
1,5
15%
Phần dành lớp đại trà
4 câu
2,5
25%
1 câu
1,0
10%
Hai tam giác bằng nhau.
Nhận biết được đâu là hai tam giác bằng nhau dựa vào hình vẽ và kí hiệu có trong hình.
Biết các trường hợp bằng nhau của hai tam giác.
Hiểu và tìm được điều kiện để chứng minh hai tam giác bằng nhau.
Viết được GT, KL của đề bài.
Phần dành lớp chọn
Vận dụng các trường hợp bằng nhau của hai tam giác để chứng minh hai tam giác bằng nhau, hai đoạn thẳng hoặc hai góc bằng nhau
Vận dụng tính chất của hai tam giác bằng nhau để chứng minh đẳng thức liên quan.
Phần dành lớp đại trà
Vận dụng các trường hợp bằng nhau của hai tam giác để chứng minh hai tam giác bằng nhau, hai đoạn thẳng hoặc hai góc bằng nhau
Vận dụng kiến thức đã học để thực hiện các bài tập nâng cao
Số câu
Số điểm
Tỉ lệ%
2 câu
0,5
5%
1 câu
0,25
2,5%
Phần dành lớp chọn
5 câu
2,75
27,5%
1 câu
1,0
10%
1 câu
1,0
10%
Phần dành lớp đại trà
5 câu
2,75
27,5%
2 câu
2,0
20%
Tam giác cân. Tam giác đều. Định lí Py – ta – go trong tam giác vuông.
Nhận biết được một tam giác là tam giác cân, tam giác đều.
Biết định lí Py – ta – go trong tam giác vuông.
Hiểu được các tính chất của tam giác cân, tam giác đều.
Tính được độ dài của một cạnh trong tam giác vuông khi biết độ dài hai cạnh còn lại.
Phần dành lớp chọn
Vận dụng các tính chất của tam giác cân, tam giác đều, định lí Py – ta – go để giải bài toán thực tế.
Vận dụng tính chất của hai tam giác bằng nhau để chứng minh đẳng thức liên quan.
Phần dành lớp đại trà
Vận dụng các tính chất của tam giác cân, tam giác đều, định lí Py – ta – go để giải bài toán thực tế.
Vận dụng kiến thức đã học để thực hiện các bài tập nâng cao
Số câu
Số điểm
Tỉ lệ%
1 câu
0,25
2,5%
2 câu
0,5
5%
1 câu
1,5
15%
Phần dành lớp chọn
4 câu
2,25
22,5%
Phần dành lớp đại trà
Tổng:
Số câu
Số điểm
Tỉ lệ
9 câu
3,0
30%
8 câu
4,0
40%
Phần dành cho lớp chọn
20 câu
10,0
100%
3 câu
3,0
30%
Phần dành lớp đại trà
20 câu
10,0
100%
3 câu
3,0
30%
Duyệt của BGH
Duyệt của Tổ CM
Nguyễn Quyền Anh
Người ra ma trận
Lê Đình Hoài
PHÒNG GD&ĐT THUẬN BẮC
TRƯỜNG THCS CAO BÁ QUÁT
(Đề chính thức 1)
ĐỀ KIỂM TRA HỌC KÌ I
NĂM HỌC: 2020 – 2021
Môn: Toán – Khối/lớp: 7
Thời gian làm bài:15 phút
(Không kể thời gian phát, chép đề)
ĐỀ:
(Đề có 02 trang)
A/-TRẮC NGHIỆM KHÁCH QUAN: (3,0 điểm) 
Khoanh tròn vào chữ cái đầu câu trả lời đúng nhất.
Câu 1: Cho y tỉ lệ thuận với x theo hệ số tỉ lệ k. 
Công thức nào sau đây biểu diễn mối liên hệ của y và x?
	A. 	B. 	C. 	D. 
Câu 2: Cho x và y là hai đại lượng tỉ lệ nghịch. Biết rằng và , hệ số tỉ lệ a bằng bao nhiêu?
	A. 2	B. 6	C. 3	D. 12
Câu 3: Một chiếc xe chạy trên một quãng đường S (km) với vận tốc v (km/h) trong thời gian là t (h). Trong ba đại lượng S, v và t, hai đại lượng tỉ lệ nghịch với nhau là:
	A. v và t	B. S và v
	C. S và t	D. Không có đại lượng nào
Câu 4: Cho hàm số . Giá trị của là:
	A. 1	B. 2	C. 3	D. 4
Câu 5: Cho x và y là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ a = 24. 
Nếu y = 6 thì giá trị của x là
	A. 30	B. 4	C. 18	D. 144
Câu 6: Cho hàm số , với x = 4 thì giá trị của y là:
Hình 1
	A. 4	B. 8	C. 12	D. 16
Câu 7: Hai tam giác bằng nhau có trong hình 1 là: 
	A. ∆ABC và ∆CDA
	B. ∆ADC và ∆BCD
	C. ∆ABC và ∆BCD
	D. ∆ADC và ∆ADB
Câu 8: Cho ∆ABC vuông tại A, công thức biểu diễn định lý Py – ta – go trong ∆ABC là:
	A. 
	B. 
	C. 
	D. 
Hình 2
Câu 9: Cho hình 2, biết rằng AE = AD và .
Giả thiết còn lại có trong hình 2 để ∆ADB = ∆AEC là:
	A. 
	B. là góc chung
	C. EC = BD
	D. AB = AC
Câu 10: Trong trường hợp bằng nhau cạnh – cạnh – cạnh của tam giác:
A. Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau.
B. Nếu hai góc và một cạnh của tam giác này bằng hai góc của tam giác kia thì hai tam giác đó bằng nhau
C. Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau
D. Nếu ba góc của tam giác này bằng ba góc của tam giác kia thì hai tam giác đó bằng nhau.
Câu 11: Nếu tam giác ABC là tam giác cân tại A thì:
	A. 	B. AB = BC	C. AC = BC	D. 
Câu 12: Cho ∆ABC đều. Khi đó:
	A. 	B. 
	C. 	D. 
--------------------------- HẾT ---------------------------
 Duyệt của BGH
Duyệt của tổ CM
Nguyễn Quyền Anh
Người ra đề
Lê Đình Hoài
PHÒNG GD&ĐT THUẬN BẮC
TRƯỜNG THCS CAO BÁ QUÁT
(Đề chính thức 1)
ĐỀ KIỂM TRA HỌC KÌ I
NĂM HỌC: 2020 – 2021
Môn: Toán – Khối/lớp: 7
Thời gian làm bài:75 phút
(Không kể thời gian phát, chép đề)
ĐỀ:
(Đề có 01 trang)
B/-TỰ LUẬN: (7,0 điểm)
I/- Phần câu hỏi chung: 
Câu 1: (1,5 điểm) Cho x và y là hai đại lượng tỉ lệ nghịch. 
Biết rằng và 
Tìm hệ số tỉ lệ a
Biểu diễn y theo x
Tính các giá trị khi biết 
Câu 2: (1,0 điểm) Cho hàm số . Tính: với 
Câu 3: (1,5 điểm) Cho tam giác ABC vuông tại A, kẻ AH ⊥ BC. Các cạnh AB = 20cm, AC = 15cm, AH = 12cm. Tính độ dài các đoạn thẳng BC, BH, CH.
II/- Phần câu hỏi riêng : 
1/- Câu hỏi dành cho học sinh đại trà : (3,0 điểm)
Câu 4: (2,0 điểm) Cho khác góc bẹt. Trên tia Ox lấy hai điểm A và C, trên tia Oy lấy hai điểm B và D sao cho OA = OB, OC = OD. Chứng minh rằng:
∆OAD = ∆OBC
AD = BC
Câu 5: (1,0 điểm) Cho hàm số với . Tìm x để y đạt giá trị nguyên.
2/- Câu hỏi dành cho học sinh lớp chọn : (3,0 điểm)
Câu 6: (2,0 điểm) Cho hình vẽ sau, chứng minh rằng:
∆ABD = ∆CAE
DE = BD + CE
Câu 7: (1,0 điểm) Tìm một số có 2 chữ số. Biết rằng chữ số hàng chục và hàng đơn vị lần lượt tỉ lệ với 2; 3 và số đó chia hết cho 3.
--------------------------- HẾT ---------------------------
 Duyệt của BGH
Duyệt của tổ CM
Nguyễn Quyền Anh
Người ra đề
Lê Đình Hoài
PHÒNG GD&ĐT THUẬN BẮC
TRƯỜNG THCS CAO BÁ QUÁT
(Đề chính thức 1)
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ I
NĂM HỌC: 2020 – 2021
Môn: Toán – Khối/lớp: 7
Thời gian làm bài:90 phút
(Không kể thời gian phát, chép đề)
ĐÁP ÁN, HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
BIỂU ĐIỂM
A. Trắc nghiệm khách quan: (3,0 điểm)
Câu 1 – B;	Câu 2 – D;	Câu 3 – A;	Câu 4 – C;	Câu 5 – B;	Câu 6 – C;
Câu 7 – A;	Câu 8 – D;	Câu 9 – B;	Câu 10 – C;	Câu 11 – D;	Câu 12 – A.
HDC: Mỗi câu trả lời đúng chấm 0,25 điểm
3,0 điểm
B/ Tự luận (7,0 điểm)
I/- Phần đáp án chung: (4,0 điểm)
Câu 1:
a) Vì x và y là hai đại lượng tỉ lệ nghịch nên: 
b) 
c) Ta có: 
Câu 2: 
Câu 3: Vẽ hình đúng được 0,25 điểm
Áp dụng định lí Py – ta – go trong tam giác ABC vuông tại A:
Vậy cm
Áp dụng định lí Py – ta – go trong tam giác ABH vuông tại H:
Vậy 
Ta có: CH = BC – BH = 25 – 16 = 4cm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
II/ Phần đáp án riêng(3,0 điểm)
1/- Phần đáp án dành cho học sinh đại trà(3,0 điểm)
Câu 4: Vẽ hình đúng được 0,5 điểm. Viết đúng GT, KL được 0,25 điểm
GT
∆OAD và ∆OBC
OA = OB; OC = OD
KL
∆OAD = ∆OBC
AD = BC
Giải: 
a) Xét ∆OAD và ∆OBC có:
OA = OB (gt)
OC = OD (gt)
 là góc chung
Vậy ∆OAD = ∆OBC (c.g.c)
b) Vì ∆OAD = ∆OBC (chứng minh trên) nên AD = BC (cặp cạnh tương ứng)
Câu 5: 
Để y đạt giá trị nguyên thì hay 
Vậy 
0,75 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
2/- Phần đáp án dành cho học sinh lớp chọn(3,0 điểm)
Câu 6: Viết đúng GT, KL được 0,25 điểm
GT
∆ABC vuông tại A
AB = AC
CE ⊥ ED; BD ⊥ ED
KL
∆ABD = ∆CAE
DE = BD + CE
Giải:
a) Ta có: (hai góc phụ nhau)
Mà: (vì )
Do đó: (cùng phụ ); (cùng phụ )
Xét ∆ABD và ∆CAE có:
AB = AC (gt)
(cmt)
(cmt)
Vậy ∆ABD = ∆CAE (g.c.g)
b) Vì ∆ABD = ∆CAE nên AE = BD; CE = AD (cặp cạnh tương ứng)
Mà DE = AE+ AD nên DE = BD + CE
Câu 7:
Gọi a, b lần lượt là chữ số hàng chục và chữ số hàng đơn vị 
Điều kiện: a, b ∈ ℕ và a, b ≤ 9
Theo đề ta có: và a + b = 3k (với )
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Vì a, b ∈ ℕ nên 3k ⋮ 5 hay k ∈ B(5) = {0; 5; 10; }
Với k = 0: không lập được số theo yêu cầu đề bài
Với k = 5: 
Suy ra a = 6 và b = 9
Với k = 10: 
Suy ra a = 20; b = 30 (Không thoả mãn điều kiện)
Vậy số cần tìm là 69
0,25 điểm
0,25 điểm
0,25 điểm
0,5 điểm
0,5 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
0,25 điểm
 Duyệt của BGH
Duyệt của Tổ CM
Nguyễn Quyền Anh
Người ra đáp án
Lê Đình Hoài